[2025-11-04] AutoEncoder

🦥 본문

정의

Unlabeled data의 효과적인 코딩을 배우는데 사용되는 인공 신경망의 한 형태. 입력 데이터를 인코딩하고 다시 디코딩하도록 훈련되는 특수한 종류의 신경망.

구조

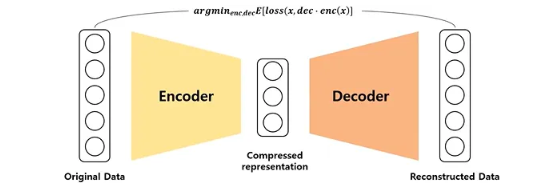
Encoder : 입력 데이터를 meaningful하고 compressed된 represntation으로 인코딩. 데이터를 요약하고 압축하여 잠재 공간으로 변환하여 가장 핵심적인 특징만 남기도록 훈련

Decoder : Encoding 된 representation을 다시 입력 데이터로 복원

• 잠재 공간 : 고차원의 원본 데이터가 압축되어 그 핵심 특징과 패턴이 저장되는 저차원의 공간

→ 입력 데이터만을 활용하는 비지도 학습으로 입력 데이터와 복원된 데이터의 차이를 최소화하는 방향으로 학습

목적

1. 입력 데이터를 의미 있고 압축된 표현으로 매핑해주는 인코더를 학습시키는 것이 목적 → manifold learning을 위한 인코더 학습. 과적합 문제를 해결하기 위함
   • 과적합 문제 : 기계 학습 모델이 훈련 데이터를 지나치게 학습하여 새롭고 본 적이 없는 데이터에 대해서는 성능이 급격하게 떨어지는 현상. 훈련 데이터에서는 완벽하지만 실제 데이터에서는 쓸모 없어짐
   • Sparse Autoencoder, Denoising Autoencoder, Contractive Autoencoder 등이 있음
2. 잠재 공간을 실제 data distribution으로 mapping 해주는 디코더를 학습시키는 것이 목적 → generative model을 위한 디코더 학습
   • Variational Autoencoder가 있음

주요 개념

• Manifold : 두 점사이의 거리 혹은 유사도가 근거리에서는 유클리디안 거리를 따르지만 원거리에서는 그러지 않는 공간.

  국소적으로는 우리가 사는 평평한 공간처럼 보이지만 전체적으로 휘어져 있거나 독특한 구조를 가질 수 있는 공간. 고차원 공간에 내재한 저차원 공간. 마치 지구.

  • manifold 가정 : 현실의 고차원 데이터는 실제로는 그 공간 전체를 채우는 것이 아니라 훨씬 낮은 차원의 숨겨진 구조를 따라 분포하고 있다는 가정. 이 숨겨진 구조를 데이터 매니폴드라고 함

    고차원 공간에 주어진 실제 세계의 데이터는 고차원 입력 공간에 내재한 훨씬 저차원 매니폴드의 인근에 집중되어 있다.

    • 태양계에 광활한 모든 위치는 데이터가 존재할 수 있는 공간임. 근데 지구라는 매니폴드 공간에만 의미 있는 데이터(생물)이 살고 있음. 그리고 그 해당 공간을 국소적으로 보면 2차원 평면처럼 보임. 그리고 표면을 따라 걸으면부드럽게 다른 의미 있는 데이터로 전환이 가능함
• Manifold Learning : 고차원 공간의 데이터를 저차원 manifold 공간으로 mapping 시키는 함수를 찾는 과정. 학습이 끝난 autoencoder의 encoder를 mapping 함수로 사용
• Generative Model : 실제 데이터 분포를 학습하여 데이터를 생성하는 생성 모델. 잠재 공간을 실제 데이터 분포로 매핑시키는 함수를 찾는 것이 목적. 학습이 끝난 Autoencoder의 decoder를 매핑 함수로 사용
• 사전 학습
  • Total Error = Bias^2 + Variance + Irreducible Error
    • Bias : 실제 데이터를 표현하는 모델과 가정한 모델의 차이에서 발생하는 오류. 실제값과 평균 예측값의 차이
    • Variance : 모델링에 사용되는 여러 표본 데이터 집합에 대한 추정을 할 때 발생하는 오류. 예측값에 대한 분산. 모델이 훈련 데이터셋의 작은 변화나 노이즈에 너무 민감하게 반응하여, 새로운 데이터셋(또는 검증셋)이 들어올 때마다 예측값의 변동(분산)이 매우 크게 나타나는 오류
    • Irreducible Error : 줄일 수 없는 자연적인 오류

    Bias와 Variance는 trade-off 관계. 차수가 높아질 수록(모델이 복잡해질 수록) Bias는 줄어들지만 Variance는 늘어남

    훈련 집합과 검증 집합 관점에서 훈련 집합에 대한 오류율이 너무 작아지면 검증 집합에 대한 variabce가 커져 과적합 발생

    → 적합한 모델의 복잡도를 찾아야 함. 복잡도를 높인 뒤, 다양한 규제 기법을 통해서 bias는 높이고 variance를 낮추는 방향으로 발전

  • 규제 : 모델에 제약을 주어서 모델이 가진 모든 용량을 사용하지 못하게 함 → 암기를 예방

• Bias-variance tradeoff in autoencoder

  데이터를 잘 복원함과 동시에(low bias) 처음 보는 데이터도 아우를 수 있는 representation을 학습(low variance)하길 바람 → 복잡도를 높이고 규제 기법을 적용

종류 : for manifold learning

1. Sparse Autoencoder : 은닉층 노드의 수가 입력층 노드의 수보다 많은 overcomplete autoencoder 구조. 은닉층에서 활성화되는 노드가 적어짐

   

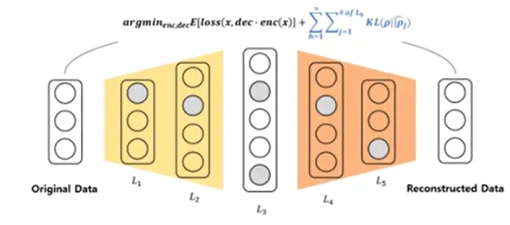
   • 일반적인 autoencoder는 입력과 복원된 출력의 차이인 재구성 오류만 최소화하는 방향으로 학습. 하지만 sparse autoencoder는 손실함수에 희소성 패널티를 추가
     • 희소성 패널티 : 잠재 공간 뉴런들의 평균 활성화 정도가 가장 낮은 값에 가깝도록 유도. 패널티를 통해 가장 중요한 특징을 포착하는 소수의 뉴런에 의존하도록 강제.

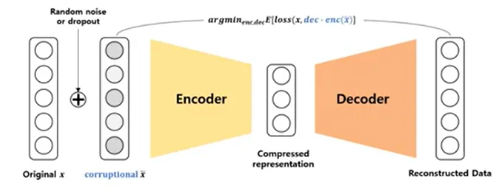
2. Denoising Autoencoder : 입력 데이터에 random noise나 dropout을 추가하는 규제 기법 적용. 입력 데이터에 어떠한 노이즈를 부여하더라도 manifold 상에서 같은 곳에 위치해야 한다는 가정. 입력데이터에 작은 변화를 주어 손상된 데이터를 만들고 모델을 통해 손상되지 않은 데이터를 출력하는 방법. 덜 민감한 강건한 모델을 만들 수 있음

   

3. Contractive Autoencoder : 작은 변화에 강건한 모델을 학습하는 것이 목적. DAE는 입력 데이터의 작은변화에 저항하는 게 중점이라면 CAE는 인코더가 디코더에서 재구성할 때 중요하지 않은 입력의 변화를 무시하도록 하여 특징을 추출할 때 작은 변화에 덜 민감하도록 중점

Application

• classification : autoencoder를 이용해 학습시킨 Encoder를 Feature extractor로 사용하여 self-supervised learning 혹은 semi-supervised learning에 활용
• clustering : unlabeled data 간에는 매니폴드가 존재
• 이상치 탐지 : 정상 관측치만을 학습 데이터로 사용하여 autoencoder가 이상 관측치는 잘 복원하지 못할 것이라는 기대 → reconstruction loss가 클 것이라 생각
• 차원 축소

import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
from torch.utils.data import random_split
import matplotlib.pyplot as plt
import numpy as np

import os
os.environ["KMP_DUPLICATE_LIT_OK"]="TRUE"

# 오토인코더 모델 클래스 생성
class Autoencoder(nn.Module):
	def __init__(self):
		super(Autoencoder, self).__init__()
		
		#Encoder
		self.encoder = nn.Sequential(
			nn.Linear(28*28, 128),
			nn.ReLU(),
			nn.Linear(128, 64),
			nn.ReLU(),
			nn.Linear(64, 16),
			nn.ReLU(),
			nn.Linear(16, 2)	# 잠재공간 latent space
		)
		
		#Decoder
		self.decoder = nn.Sequential(
			nn.Linear(2, 16),
			nn.ReLU(),
			nn.Linear(16, 64),
			nn.ReLU(),
			nn.Linear(64, 128),
			nn.ReLU(),
			nn.Linear(128, 28*28),
			nn.Sigmoid()
		)
	# 순전파
	def forward(self, x):
		x_encoded = self.encoder(x) # x_encoded: 입력으로 주어진 784차원을 잠재 차원으로 줄인 값
		x = self.decoder(x_encoded)
		return x, x_encoded

# =============================
# --- MNIST 데이터셋 학습 준비 ---
# =============================
# 데이터 변환
transform = transforms.Compose([
	transforms.ToTensor(),
])

# 원본 학습 데이터셋 로드
full_train_dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)

# 학습 데이터셋을 train, validate로 분리 (8:2)
train_size = int(0.8 * len(full_train_dataset))
val_size = len(full_train_dataset) - train_size
train_subset, val_subset = random_split(full_train_dataset, [train_size, val_size])

# 학습데이터, 검증데이터 로드 
train_loader = DataLoader(train_subset, batch_size=32, shuffle=True)
val_loader = DataLoader(val_subset, batch_size=1000, shuffle=False)

# 테스트 데이터 로드
test_dataset = datasets.MNIST(root='./data', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, batch_size=1000, shuffle=True)

# ============================
# --- AutoEncoder 학습 진행 ---
# ============================
print(f"\n===== Training Autoencoder with 2D Latent Space =====")

# 모델, 손실 함수, 옵티마이저 초기화
model = Autoencoder()
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=1e-3)
num_epochs = 60

train_losses = []
val_losses = []

# 학습 루프
for epoch in range(num_epochs):
    model.train()
    running_train_loss = 0.0
    for data in train_loader:
        img, _ = data
        img = img.view(img.size(0), -1)
        output, _ = model(img)
        loss = criterion(output, img)
        
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        running_train_loss += loss.item()
    
    epoch_train_loss = running_train_loss / len(train_loader)
    train_losses.append(epoch_train_loss)

    # --- 검증 단계 ---
    model.eval()
    running_val_loss = 0.0
    with torch.no_grad():
        for data in val_loader:
            img, _ = data
            img = img.view(img.size(0), -1)
            output, _ = model(img)
            loss = criterion(output, img)
            running_val_loss += loss.item()
    
    epoch_val_loss = running_val_loss / len(val_loader)
    val_losses.append(epoch_val_loss)

    # 에포크마다 손실과 검증 수치 출력
    print(f'Epoch [{epoch+1}/{num_epochs}], Train Loss: {epoch_train_loss:.4f}, Val Loss: {epoch_val_loss:.4f}')

print("Training Complete")

# 손실 시각화
plt.figure(figsize=(10, 5))
plt.plot(train_losses, label='Training Loss')
plt.plot(val_losses, label='Validation Loss')
plt.title('Training & Validation Loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.grid(True)
plt.show()

# ==========================================================
# --- 모델 복원도 평가 (테스트 데이터셋 전체에 대한 평균 손실 계산) ---
# ==========================================================
model.eval()
test_loss = 0.0
with torch.no_grad():
    for data in test_loader:
        imgs, _ = data
        imgs = imgs.view(imgs.size(0), -1)
        outputs, _ = model(imgs)
        loss = criterion(outputs, imgs)
        test_loss += loss.item()
test_loss /= len(test_loader)
print(f"\n--- Results for 2D Model ---")
print(f"복원도 (Average Test Loss): {test_loss:.4f}\n")

print(f"Visualizing reconstructed images for 2D model...")

# ================================
# --- 실제 데이터셋을 이용한 테스트 ---
# ================================
# 테스트 데이터
dataiter = iter(test_loader)
images, _ = next(dataiter)
images_flattened = images.view(images.size(0), -1)

# 테스트 데이터를 학습시킨 AutoEncoder를 통해 테스트
output, _ = model(images_flattened)
output = output.view(output.size(0), 1, 28, 28).detach()

# 결과 시각화
fig, axes = plt.subplots(nrows=2, ncols=10, sharex=True, sharey=True, figsize=(20,4))
fig.suptitle(f'Reconstruction Results (2D Latent Space)')
# 원본 이미지
for i in range(10):
    img = images[i].squeeze()
    axes[0,i].imshow(img.numpy(), cmap='gray')
    axes[0,i].get_xaxis().set_visible(False)
    axes[0,i].get_yaxis().set_visible(False)
    if i == 0: axes[0,i].set_title('Originals', loc='left')

# 복원된 이미지
for i in range(10):
    img = output[i].squeeze()
    axes[1,i].imshow(img.numpy(), cmap='gray')
    axes[1,i].get_xaxis().set_visible(False)
    axes[1,i].get_yaxis().set_visible(False)
    if i == 0: axes[1,i].set_title('Reconstructed', loc='left')
plt.show()

# ============================
# --- latent vactors 시각화 ---
# ============================
model.eval()	# 모델을 평가 모드로 변경

latent_vectors = []
labels = []

with torch.no_grad():
	for data in test_loader:
		imgs, lbls = data
		imgs = imgs.view(imgs.size(0), -1)
		_, latents = model(imgs)
		latent_vectors.append(latents)
		labels.append(lbls)
		
latent_vectors = torch.cat(latent_vectors, dim=0)
labels = torch.cat(labels, dim=0)

# 2D 시각화
plt.figure(figsize=(12, 10))
# 각 숫자 레이블(0-9)에 대해 다른 색상으로 산점도 그리기
for i in range(10):
	indices = labels == i
	plt.scatter(latent_vectors[indices, 0], latent_vectors[indices, 1], label=str(i), alpha=0.7, s=15)

plt.xlabel('Latent X')
plt.ylabel('Latent Y')
plt.title('2D Latent Space Visualization')
plt.legend()
plt.grid(True)
plt.show()

# =======================================
# --- 3차원 이상의 latent vector 확인 시 ---
# =======================================
"""
from sklearn.manifold import TSNE

# t-SNE 적용
tsne = TSNE(n_components=2, perplexity=30, max_iter=300)
tsne_result = tsne.fit_transform(latent_vectors)

# 시각화
plt.figure(figsize=(20, 8))

# t-SNE 결과 플롯
for i in range(10):
    indices = labels == i
    plt.scatter(tsne_result[indices, 0], tsne_result[indices, 1], label=str(i), alpha=0.7, s=15)
plt.title('t-SNE Visualization of Latent Space')
plt.xlabel('t-SNE Dimension 1')
plt.ylabel('t-SNE Dimension 2')
plt.legend()
plt.grid(True)

plt.show()
"""

• def __init__(self): 생성자
  • super(Autoencoder, self).__init__() : 부모 생성자 상속, 명시적으로 해당 객체와 클래스를 파라미터로 넣음
  • self.encoder, self.decoder: 인코더 및 디코더
    • nn.Sequential() : 여러 개의 신경망 레이어들을 순차적으로 묶어 하나의 모듈로 만드는 데 사용하는 클래스이자 메소드
    • nn.Linear() : 입력 데이터를 가중치 행렬과 곱하고 편향을 더하는 선형 변환을 수행. 해당 파라미터만큼 압축 784 → 128 → 64 → 16 → 2
    • nn.ReLU() : 입력이 0보다 크면 그대로 출력, 0보다 작으면 0 출력
    • nn.Sigmoid() : 입력을 0과 1 사이의 값으로 압축
• def forward(self, x) : 인코딩 - 디코딩 과정을 수행
  • x : 텐서값
  • x_encoded : 잠재 차원으로 압축한 값
• transform : 함수처럼 작동하는 객체. callable object
  • transforms.Compose() : 여러 개의 변환 작업을 하나의 순차적인 파이프라인으로 묶어줌
  • transforms.ToTensor() : 이미지를 텐서 형식으로 변환
• full_train_dataset : 호출되어 만들어진 객체는 데이터셋의 전체 학습 데이터를 메모리에 바로 올리는 대신 인터페이스를 할당. 파라미터로 데이터를 어떻게 불러올지 결정
  • transform 객체를 통해 전처리
• train_loader, val_loader : 학습 데이터, 검증 데이터 로드
  • DataLoader() : 데이터 로더 클래스, 데이터 객체를 받아 모델이 처리하기 쉬운 배치 단위로 제공해주는 반복자를 생성
• Optimizer : 모델이 계산한 손실을 최소화하기 위해, 각 가중치를 어떤 방향으로 얼마나 크게 조정해야하는 지 결정하는 알고리즘
• 학습 루프
  • epoch : 전체 데이터 셋을 학습하는 횟수
  • model.train() : 학습 모드로 설정. 학습 모드로 설정해야 계산 및 업데이트를 활성화
  • for data in train_loader : DataLoader()를 통해 배치 단위로 데이터셋을 로드하게 됨
    • img, _ = data : data는 32개의 이미지와 32개의 레이블을 담고 있는 튜플 형태. _를 통해 이미지만 img에 할당되고 레이블은 무시됨.
    • img = img.view(img.size(0), -1) : nn.Linear()에 입력되기 위해 평탄화
    • output과 img를 손실 함수에 넣어서 재구성 오류를 계산.
    • optimizer.zero_grad() : 이전 이터레이션에서 계산된 가중치의 기울기를 0으로 초기화
    • loss.backward() : 역전파를 통해 가중치가 오류에 얼마나 기여했는지 기울기 계산
    • optimizer.step() : 계산된 기울기와 학습률을 이용하여 모델의 모든 가중치 계산
    • running_train_loss += loss.item() : 해당 에포크의 총 손실률을 구하기 위해 배치 단위에서 손실률 합함
  • epoch_train_loss : 해당 에포크의 평균 손실을 계산하고 그래프 시각화를 위해 평균 손실값을 목록에 추가
  • 검증 단계를 통해 에포크마다 검증을 진행